Heap

Heap

A Heap (uppercase ‘H’) is a general concept of a tree-based data structure that satisfies the “heap property.”

• A Binary Heap is the most common and widely used implementation of a Heap, and has additional requirements.
• When people say “heap” in a data structures class, they almost always mean a binary heap, unless they explicitly say otherwise.

Max and Min heap

• A “Heap” in DSA is a specialized tree-based data structure that adheres to the heap property. This property dictates the relationship between a parent node and its children.
• There are two main types of heaps based on this property:

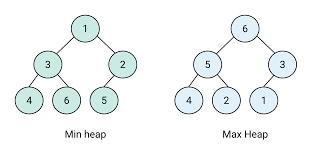
1. Max-Heap: For every node, the value of the parent node is greater than or equal to the values of its children. This means the largest element is always at the root.
2. Min-Heap: For every node, the value of the parent node is less than or equal to the values of its children. This means the smallest element is always at the root.

Characteristics

• Heap Property: As described above (either Max-Heap or Min-Heap).
• Partial Order: Unlike a Binary Search Tree (BST) which is fully ordered, a heap is only partially ordered. You only know the relationship between a parent and its direct children, not necessarily between siblings or elements at different levels (except for the root being the min/max).
• Used for Priority Queues: Heaps are the go-to data structure for implementing a priority queue, where elements are retrieved based on their priority (highest or lowest).