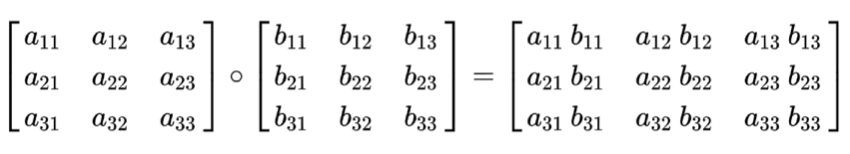What it does (an overview)

Vectors and matrices
- In NumPy, vectors will be 1D (most of the time)
  - In other conventions a vector is treated as 2D
Common operations in vectors and matrices
- Dot Product/Inner product
  - $a \cdot b = a^{T} b = \sum_{d = 1}^{D} a_{d} b_{d}$
  - $a \cdot b = a_{1} b_{1} + a_{2} b_{2} + a_{3} b_{3}$
  - Takes 2 vectors, multiplies them element wise, then add those products together
  - Both input vectors must have the same shape
- Matrix multiplication
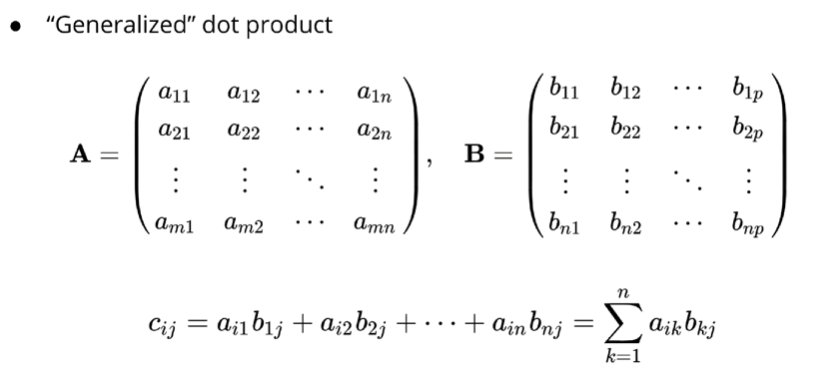
  - Just doing a bunch of mini dot products
  - Dot row 1 of $a$ and column 1 of $b$ and so on
  - Number of columns of a = Number of rows of b
    - Inner dimensions must match
- Element-wise product
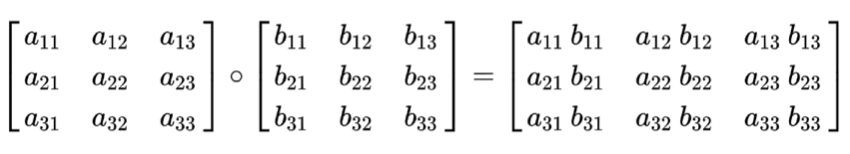
  - Not so common in linear algebra, but very common in ML
- We can solve linear systems (solving for x)
  - $A x = b$
- Inverse: $A^{- 1}$
- Determinant: $∣ A ∣$
- Choosing random number/matrix from distribution (eg. Uniform, Gaussian)

leejunkim